聊聊go-metrics中Meter的设计实现
版权声明 本站原创文章 由 萌叔 发表
转载请注明 萌叔 | https://vearne.cc
引言
我们的打算对某个golang的服务,统计一下它每秒的QPS, go-metrics成为我们不二的选择。
在我的文章METRICS的简易实现
我简单的给出了对这个问题的一种简易实现。
1. 简易实现的优缺点
优点
1) 实现方式相对直观
缺点
为了一个指标,所带来的开销很大
1) 每个指标需要1个专门的协程,每秒钟做一次"快照"
2) 1分的的QPS需要60个点, 如果还需要5分钟, 15分钟的QPS
那么共需记录 60 * (1 + 5 + 15) = 1260 个点
2. go-metrics的实现
传送门
meter.go
2.1 理论
go-metrics中对于Meter的实现基于EWMA(Exponentially Weighted Moving-Average) 中文译为指数加权移动平均法
它是一种特殊的加权移动平均法。其特点是: 第一,指数平滑法进一步加强了观察期近期观察值对预测值的作用,对不同时间的观察值所赋予的权数不等,从而加大了近期观察值的权数,使预测值能够迅速反映市场实际的变化。权数之间按等比级数减少,此级数之首项为平滑常数a,公比为(1- a)。第二,指数平滑法对于观察值所赋予的权数有伸缩性,可以取不同的a 值以改变权数的变化速率。如a取小值,则权数变化较迅速,观察值的新近变化趋势较能迅速反映于指数移动平均值中。因此,运用指数平滑法,可以选择不同的a 值来调节时间序列观察值的均匀程度(即趋势变化的平稳程度)。
EWMA 在实际应用中,主要是用于预测股价变化等等
注意 下面公式中的λ和上面文献中的a 是同一个参数,特此说明
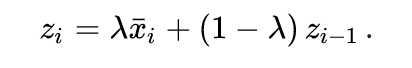
预测的方法是,每隔一段时间进行一次采样,每次采样完成之后,就对预测值进行一次修正,这种方法的特点是近期的采样值对预测值的影响大,远期的影响较小
这种理论是有合理性的,尤其是对于了连续变化的曲线
2.2 实现
meter.go 中,重要的结构有2个
type StandardMeter struct {
lock sync.RWMutex
snapshot *MeterSnapshot
a1, a5, a15 EWMA
startTime time.Time
stopped bool
}
// 定时调用StandardMeter的tick方法
type meterArbiter struct {
sync.RWMutex
started bool
meters map[*StandardMeter]struct{}
ticker *time.Ticker
}
func NewMeter() Meter {
if UseNilMetrics {
return NilMeter{}
}
m := newStandardMeter()
arbiter.Lock()
defer arbiter.Unlock()
arbiter.meters[m] = struct{}{}
if !arbiter.started {
arbiter.started = true
go arbiter.tick()
}
return m
}
a1, a5, a15 的唯一区别是λ 值不同
// NewEWMA1 constructs a new EWMA for a one-minute moving average.
func NewEWMA1() EWMA {
return NewEWMA(1 - math.Exp(-5.0/60.0/1))
}
// NewEWMA5 constructs a new EWMA for a five-minute moving average.
func NewEWMA5() EWMA {
return NewEWMA(1 - math.Exp(-5.0/60.0/5))
}
arbiter 作为模块变量,会统一的管理所有Meters,每5秒计算一下平均值(采样点),并让MeterSnapshot中的计数器清零,重新开始计数
var arbiter = meterArbiter{ticker: time.NewTicker(5e9), meters: make(map[*StandardMeter]struct{})}
总结
显然基于EWMA的方法,对于每一个Meter都只需要一个计数器即可,内存消耗大大降低了。
参考资料
请我喝瓶饮料
