聊聊布隆过滤器

版权声明 本站原创文章 由 萌叔 发表
转载请注明 萌叔 | https://vearne.cc

1. 前言

笔者早几年的工作经历和爬虫相关，为防止重复抓取URL, 要对每个需要抓取的URL进行判重，由于每天待抓取的URL数量都在好几亿条。因此去重服务的压力很大，当时相关的小伙伴就曾经调研过布隆过滤器。
本文笔者将结合Google Guava的BloomFilter(com.google.common.hash.BloomFilter)，谈谈布隆过滤器的实现，以及它的一些特点。

2. 布隆过滤器简介

An empty Bloom filter is a bit array of m bits, all set to 0. There must also be k different hash functions defined, each of which maps or hashes some set element to one of the m array positions, generating a uniform random distribution.

布隆过滤器由一个m位的bitArray以及k个hash函数组成。m和k的具体值可以由布隆过滤器中预期存储的数据量n，以及可能出现假阳性概率p决定。

待存储的数据经过1个hash函数作用，并会将bitArray中的某一位置成1
k个hash函数最多会将bitArray中k位置成1

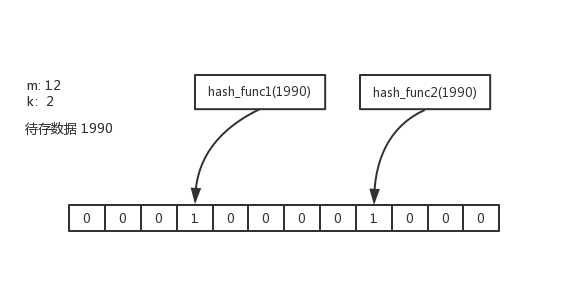
如上图所示,假定k=2
hash_func1将bitArray[3]=1
hash_func2将bitArray[8]=1

如果想判断数值1990是否在布隆过滤器中，只需要重新执行hash_func1和hash_func2，如果第3位和第8位都是1，那么1990可能在布隆过滤器中(存在假阳性的可能)，反之第3位和第8位有1位为0，则1990一定不在布隆过滤器中。

可以换一个角度来解释布隆过滤器，每个hash函数都在尝试提取数据值的一部分特征。存储数据的过程(置1)，实际是在标记，布隆过滤器中至少包含一个元素满足特定的特征。如果有一个特征不满足，那么该数据一定不在布隆过滤器中。

举个例子满足以下特征的就是哺乳动物

• 身体表面有毛
• 用肺呼吸
• 体温恒定
• 哺乳
• 胎生

有一个特征不满足，肯定不是哺乳动物
从这里我们能够想到，布隆过滤器准确性很大程度上依赖于hash函数的选取，只有hash选择的合适才能够提取出数据值的特征。

3. Google Guava的BloomFilter

首先来看看BloomFilter 使用示例

package guava;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;

public class TestBloomFilter {

    static long optimalNumOfBits(long n, double p) {
        if (p == 0) {
            p = Double.MIN_VALUE;
        }
        return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
    }

    static int optimalNumOfHashFunctions(long n, long m) {
        // (m / n) * log(2), but avoid truncation due to division!
        return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
    }

    public static void main(String args[])
    {
        int n = 10000;
        float p = 0.01f;
        long m = optimalNumOfBits(n, p);
        System.out.println("optimalNumOfBits:" + m);
        System.out.println("optimalNumOfHashFunctions:" + optimalNumOfHashFunctions(n, m));

        BloomFilter<Integer> filter = BloomFilter.create(Funnels.integerFunnel(), n, p);
        for(int i=0;i<n*5;i++){
            filter.put(i*2);
        }
        int success = 0;
        int failed = 0;
        for(int i=2000;i<3000;i++){
            if (filter.mightContain(i) && i%2 ==0){
                success++;
            }
            if (filter.mightContain(i) && i%2 !=0){
                failed++;
            }
        }
        System.out.println(1- (success + 0.0)/(success + failed));
    }
}

create(Funnel<? super T> funnel, int expectedInsertions, double fpp)

创建空的BloomFilter
funnel: 数据类型
原生BloomFilter已经支持了int,String等数据类型，其它也可以通过实现Funnel接口来满足
expectedInsertions: 预期将存入的数据量, 相当于n
fpp: 能够承受的假阳性的概率

• 预期存储的数据量n越大，bitArray的位数m越大, hash函数的个数k越大
• fpp 越小，bitArray的位数越大

3.1 空间开销

我们来做个简单的定量分析

n	p	m	k	false positive probability(%)
10k	0.01	95850 约为11KB	7	1.38
100k	0.01	958505 约为119KB	7	0.39
100M	0.01	958505842 约为120MB	7	0.99

HashMap假定HashMap的装载系数为0.75，同样存储10k个数据，数据为int类型，则

10000 * 4 / 0.75 /1000 约需要53KB的空间

可见相比与HashMap, BloomFilter节约了将近80%的空间开销。当然BloomFilter有假阳性问题，但这个问题在很多场景下是可以接受的。
另外我们能看到k几乎没有变化，可认为是常数。因此写入和判重的时间复杂度是O(1)

3.2 特点2

Guava的BloomFilter的只能存数据，无法删除一个数据。
并且如果BloomFilter的数量超过expectedInsertions, 则假阳性的概率会上升
expectedInsertions:10k
fpp: 0.01

realInsertions	false positive probability(%)
10k	1.38
20k	16.0
30k	31.5
40k	40.5

超过3倍expectedInsertions, BloomFilter几乎已经没法用了

4. 源码分析

在Google Guava的BloomFilter的实现中比较重要的有

预估bitArray的位数`m`
optimalNumOfBits()
预估hash函数的个数`k`
optimalNumOfHashFunctions()

写入数据
put()
判断是否包含
mightContain()

BloomFilterStrategies.MURMUR128_MITZ_64

 MURMUR128_MITZ_64() {
    @Override
    public <T> boolean put(
        T object, Funnel<? super T> funnel, int numHashFunctions, LockFreeBitArray bits) {
      long bitSize = bits.bitSize();
      byte[] bytes = Hashing.murmur3_128().hashObject(object, funnel).getBytesInternal();
      long hash1 = lowerEight(bytes);
      long hash2 = upperEight(bytes);

      boolean bitsChanged = false;
      long combinedHash = hash1;
      for (int i = 0; i < numHashFunctions; i++) {
        // Make the combined hash positive and indexable
        bitsChanged |= bits.set((combinedHash & Long.MAX_VALUE) % bitSize);
        combinedHash += hash2;
      }
      return bitsChanged;
    }

    @Override
    public <T> boolean mightContain(
        T object, Funnel<? super T> funnel, int numHashFunctions, LockFreeBitArray bits) {
      long bitSize = bits.bitSize();
      byte[] bytes = Hashing.murmur3_128().hashObject(object, funnel).getBytesInternal();
      long hash1 = lowerEight(bytes);
      long hash2 = upperEight(bytes);

      long combinedHash = hash1;
      for (int i = 0; i < numHashFunctions; i++) {
        // Make the combined hash positive and indexable
        if (!bits.get((combinedHash & Long.MAX_VALUE) % bitSize)) {
          return false;
        }
        combinedHash += hash2;
      }
      return true;
    }

这里比较有意思的是
1）MURMUR128_MITZ_64使用的Murmur哈希，它与其它流行的哈希函数相比，对于规律性较强的key，MurmurHash的随机分布特征表现更良好。在前文笔者提到布隆过滤器准确性很大程度上依赖于hash函数的选取，所以这里选择了MurmurHash是有原因的。
2) k个hash函数其实是由2个hash函数演变来的

hash_func_i(x) = (hash_func1(x) + i * hash_func2(x) ) % m
1 <= i <= k

5. 总结

布隆过滤器和hyperloglog一样都是从概率方法上对集合数据结构进行的空间优化，前者用来判重，后者用来计数。他们在使用场景上，都一定局限性。但对于特定场景，空间和时间复杂度都非常的低，可以达到四两拨千斤的效果。

后记

2022年8月24日
n、p、m、k对布隆过滤器的计算影响可以看这个链接here

参考资料

1. wikipedia-Bloom filter
2. wikipedia-布隆过滤器
3. Google Guava之BloomFilter源码分析及基于Redis的重构
4. Murmur哈希

---