火车票购票问题1
版权声明 本站原创文章 由 萌叔 发表
转载请注明 萌叔 | https://vearne.cc
前段时间看了知乎的一篇文章
12306 外包给阿里巴巴、IBM 等大企业做是否可行?
李爱吉对于买票问题的优化算法,给了我非常大的启示,我决定实现出来,以享众人。
1.火车票购票问题描述
假定该车次有s1、s2、s3 ... 到s6个站点,共6个站点
对于任意一个座位,初始时它可以出售的有效区间都是从首站s1到末站sN, 但是如果该座位某一段被售出,能出售有效区间就变化了。
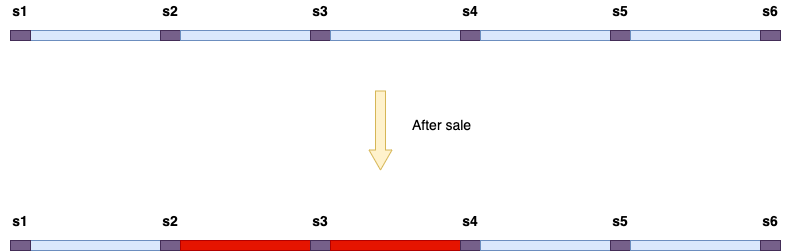
如果上图所示:
红色的区段表示已经售出,该座位的情况是
- 站点2 -> 站点4 的票已经被售出
- 站点1 -> 站点2 的票仍可售卖
- 站点4 -> 站点6 的票仍可售卖
以某趟车次的车票出售为例,假定该车次有20节车厢,每节车厢有100个座位,那么共有座位 100 * 20 = 2000座位
那么在购票时(从站点x到站点y),都必须遍历这2000个座位,以找到一个合适的座位,由于有的座位的某些区段已经被售出,实际遍历的查询次数肯定大于2000次
这里把座位数记为m
查询n次的时间复杂度就是O(mn)
2. 查询优化
假定某趟车次共有10个站点,那么根据排列组合,能够售出车票,出发站、到达站的组合只能有 10 *(10 - 1) / 2 = 45 种
优化方法:
由于组合是有限的,我们可以把每个座位可以售卖的站点区间索引起来,当一个购票请求(x,y)从站点x到站点y 到达时,首先去查询
对应站点区间是否有票,如果没有就尝试在能够覆盖(x,y) 的站点区间的索引中去寻找。
# -*- coding: utf-8 -*-
############################################################
# 假定站点编号从 1 ~ 10
# 共20节车厢, 每个车厢20排
# 编号形如
# 1A 1B 1C 1D 1F
# 2A 2B 2C 2D 2F
# ...
# 20A 20B 20C 20D 20F
# 20 * 5 * 20 = 2000个座位
# 其实座位编号完全可以从 0 ~ 1999, 并不影响我们对问题本身的分析
############################################################
import time
MAX_CARRIAGE_NUM = 20
MAX_ROW_NUM = 20
MAX_SITE_INDEX = 10
class Seg(object):
def __init__(self, carriage_no, seat_no, start_site, end_site):
# 车厢编号
self.carriage_no = carriage_no
# 座位编号
self.seat_no = seat_no
# 完整编号
self.no = str(carriage_no) + '-' + seat_no
# 能够售卖的开始站序号 int
self.start_site = start_site
# 能够售卖的终点站序号 int
self.end_site = end_site
def __str__(self):
return str((self.no, self.start_site, self.end_site))
def init():
ticket_dict = {}
for i in range(1, MAX_SITE_INDEX):
for j in range(i + 1, MAX_SITE_INDEX + 1):
ticket_dict[(i, j)] = []
for i in range(1, MAX_CARRIAGE_NUM + 1):
for row in range(1, MAX_ROW_NUM + 1):
for col in ['A', 'B', 'C', 'D', 'F']:
# 每个座位都可以出售从s1 到 s10的车票
key = (1, 10)
# print Seg(i, str(row) + col, 1, 10)
ticket_dict[key].append(Seg(i, str(row) + col, 1, 10))
return ticket_dict
def sell(ticket_dict, start, end):
'''
:param ticket_dict:
:param start: 购票的起始站
:param end: 购票的终点站
:return:
'''
# 需要找到一个有票的站点区间覆盖目标站点区间
# 所有可能的起始站
site_start = []
x = 1
while x <= start:
site_start.append(x)
x += 1
site_start.reverse()
# 所有可能的终点站
site_end = []
y = end
while y <= MAX_SITE_INDEX:
site_end.append(y)
y += 1
# print 'site_start', site_start
# print 'site_end', site_end
for x in site_start:
for y in site_end:
ticket = None
if len(ticket_dict[(x, y)]) > 0:
ticket = ticket_dict[(x, y)].pop()
if ticket:
# 判断一下这个座位的站点区间是否被完全用完了
# 如果没有还需要把新生成的余票间存回去
if start > x:
temp = Seg(ticket.carriage_no, ticket.seat_no, x, start)
ticket_dict[(x, start)].append(temp)
if y > end:
temp = Seg(ticket.carriage_no, ticket.seat_no, end, y)
ticket_dict[(end, y)].append(temp)
return Seg(ticket.carriage_no, ticket.seat_no, start, end)
return None
def print_residual(ticket_dict):
print '------------余票情况-------------'
for key in ticket_dict:
if ticket_dict[key]:
print key, len(ticket_dict[key])
if __name__ == '__main__':
ticket_dict = init()
t1 = time.time()
with open('req.csv') as fp:
for line in fp:
ll = line.split(',')
user = ll[0]
start = int(ll[1])
end = int(ll[2])
ticket = sell(ticket_dict, start, end)
if ticket:
print '#' * 100
print line.strip()
print user, "bought", ticket
print_residual(ticket_dict)
# time.sleep(2)
t2 = time.time()
print t2 - t1
我随机生成了一个测试文件req.csv 来模拟用户的购票行为, 测试结果表明, 及时在单线程的情况下,只用了不到2秒就处理完了10w
个请求。这个速度已经足够快了,下一次我们再来对程序进行优化。
完整代码地址:
https://github.com/vearne/train_ticket
后记:
方法1 是从座位出发寻找有效的车票
最好情况下的时间复杂度是
O(mn) m是座位数,n是查询次数
方法2 是从站点区间出发寻找有效的车票
最坏情况下的时间复杂度是
$O(k(k-1)/2n)$ 约等于 $O(k^2*n)$
假设某趟列车共有1000个座位,涉及10个站点,可以推算出,方法2几乎比方法1快了一个数量级。
