算法题 LEECODE 313. 超级丑数
版权声明 本站原创文章 由 萌叔 发表
转载请注明 萌叔 | https://vearne.cc
题目
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/super-ugly-number
编写一段程序来查找第 n 个超级丑数。超级丑数是指其所有质因数都是长度为 k 的质数列表 primes 中的正整数。
示例
输入: n = 12, primes = [2,7,13,19]
输出: 32
解释: 给定长度为 4 的质数列表 primes = [2,7,13,19],前 12 个超级丑数序列为:[1,2,4,7,8,13,14,16,19,26,28,32]。
说明:
1 是任何给定 primes 的超级丑数。
给定 primes 中的数字以升序排列。
0 < k ≤ 100, 0 < n ≤ 106, 0 < primes[i] < 1000 。
第 n 个超级丑数确保在 32 位有符整数范围内。
解题思路1
由于这是一道中等难度的题目,萌叔第一想到的是穷举,从1开始穷举,1、2 3、... N 判断每个数是否是超级丑数。这个思路肯定是没错的,结果提交后发现超时了。超时的原因是扫描了太多无用的数据。
解题思路2
超级丑数是指其所有质因数都在primes 列表中, 那么很容易可以想到,可以用primes列表中的质数来构造超级丑数。现在唯一麻烦的是怎么按照超级丑数的大小来定序。
查找第 n 个超级丑数,也就是要从整个解空间中,找出第N大的超级丑数。
我们先来看看解空间有什么特点。
为了简化图表,假定primes = [2,7,13,19],1是比较特殊的情况,跳过不看
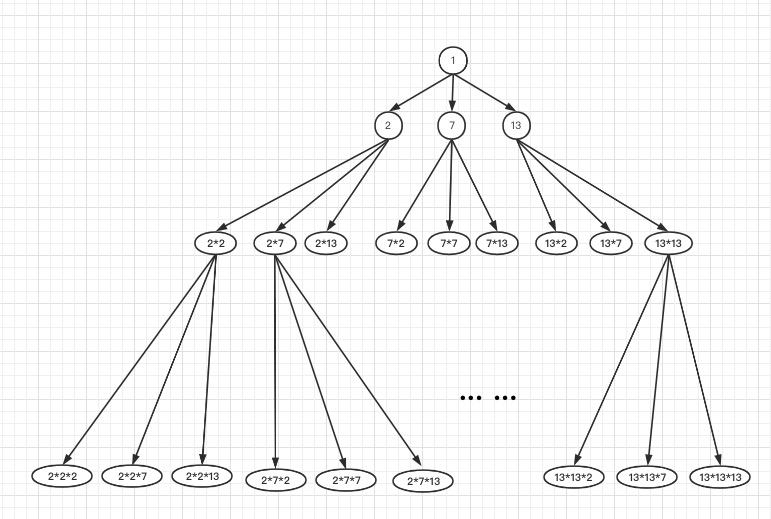
- 解空间是一颗多叉数
- 从根沿着树干节点向下,节点的数值越来越大
- 每个节点的孩子节点,都是它的值乘以
primes中的每个数 - 当前的最小值,可能在多个子树中产生
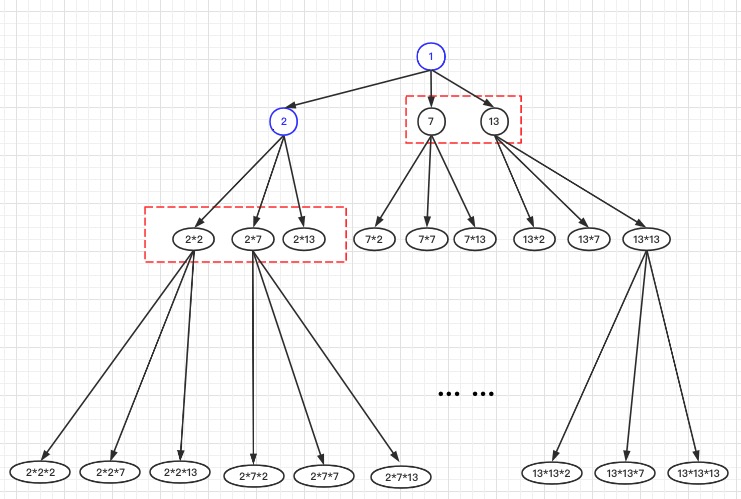
某一时刻,假定我们已经找到了超级丑数1、 2,我们把1、2、从树中移除,可以得到若干个新的子树,新的子树的根节点分别是
2*2、 2*7、 2*13、 7、 8,下一个最小的超级丑数,只能从这几个数产生。因为剩下的节点都是以上节点的子孙节点,所以肯定要比这些节点中最小值还要大。
思路确定
每次从解空间中找到一个超级丑数,就从把它从多叉树上移除,然后扫描剩余多个子树的根节点,确定下一个超级丑数。为了加快扫描的速度,已知的子树的根,都存储在一个小顶堆里。
递推公式
f(n) = min(f(n -1)的子节点, 其它子树的根)
代码如下
package main
import (
"container/heap"
"fmt"
)
// An IntHeap is a min-heap of ints.
type IntHeap []int
func (h IntHeap) Len() int { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *IntHeap) Push(x interface{}) {
// Push and Pop use pointer receivers because they modify the slice's length,
// not just its contents.
*h = append(*h, x.(int))
}
func (h *IntHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
func nthSuperUglyNumber(n int, primes []int) int {
h := IntHeap([]int{})
heap.Push(&h, 1)
for _, value := range primes {
heap.Push(&h, value)
}
idx := 0
last := 0
var t int
for len(h) > 0 && idx < n {
t = heap.Pop(&h).(int)
// 解决冗余数据
for t <= last {
t = heap.Pop(&h).(int)
}
last = t
for _, v := range primes {
heap.Push(&h, v*last)
}
idx++
}
return last
}
func main() {
n := 550
primes := []int{3, 7, 17, 19, 23, 29, 31, 37, 43,
47, 59, 67, 71, 73, 83, 97, 103, 109, 127, 131, 139, 149, 163, 167, 173, 191, 197, 233, 241, 251}
fmt.Println(nthSuperUglyNumber(n, primes))
}
请我喝瓶饮料
