使用遗传算法来解决旅行商问题

版权声明 本站原创文章 由 萌叔 发表
转载请注明 萌叔 | https://vearne.cc

1. 前言

一直对遗传算法非常好奇，它是对自然界生物进化机制的计算机模拟。可以用于对NP问题的最优化求解。
在生活中，可以被用于排班、排课、路径优化，甚至可以被用于歌曲自动编写。

2. 问题分析

遗传算法的一个典型案例是针对旅行商问题。 旅行商问题，一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

我们从一个最简单的情况来说明这个问题。

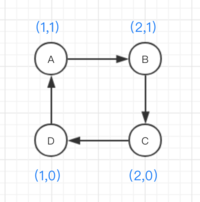
例1：假定有A、B、C、D四个地点，坐标如上图
假定出发点是A点，那么所有的可能的路径是

• ABCDA
• ABDCA
• ACBDA
• ACDBA
• ADBCA
• ADCBA

由于起点和终点都是A，是完全确定的；所以所有可能的路径就是B、C、D的全排列
共有n!中情况，此处n为3，共有6种情况
我们实际是在解空间中寻找最优解。
当n=20时
20！= 2,432,902,008,176,640,000
当n=21时，解空间的大小已经溢出了int64所能存储的空间
解空间相当大，以至于遍历一遍几乎是不大可能的

3. 遗传算法如何寻找最优解

事实上，遗传算法得到有可能得到最优解，也有可能得到次优解。

下面是遗传算法的完整过程

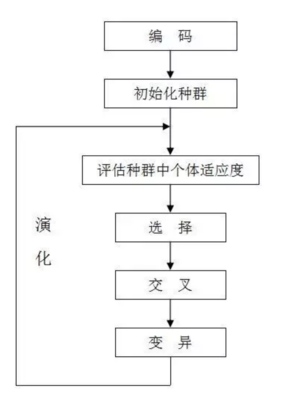
3.1 编码

让我们再回到例1，由于只有6种情况，那么解空间的取值范围就是 [0, 5]
假定如下的对应关系

• BCD -- 0 -- 000
• BDC -- 1 -- 001
• CBD -- 2 -- 010
• CDB -- 3 -- 011
• DBC -- 4 -- 100
• DCB -- 5 -- 101

解被转换为数值以后，就可以使用2进制进行表示

3.2 初始化种群

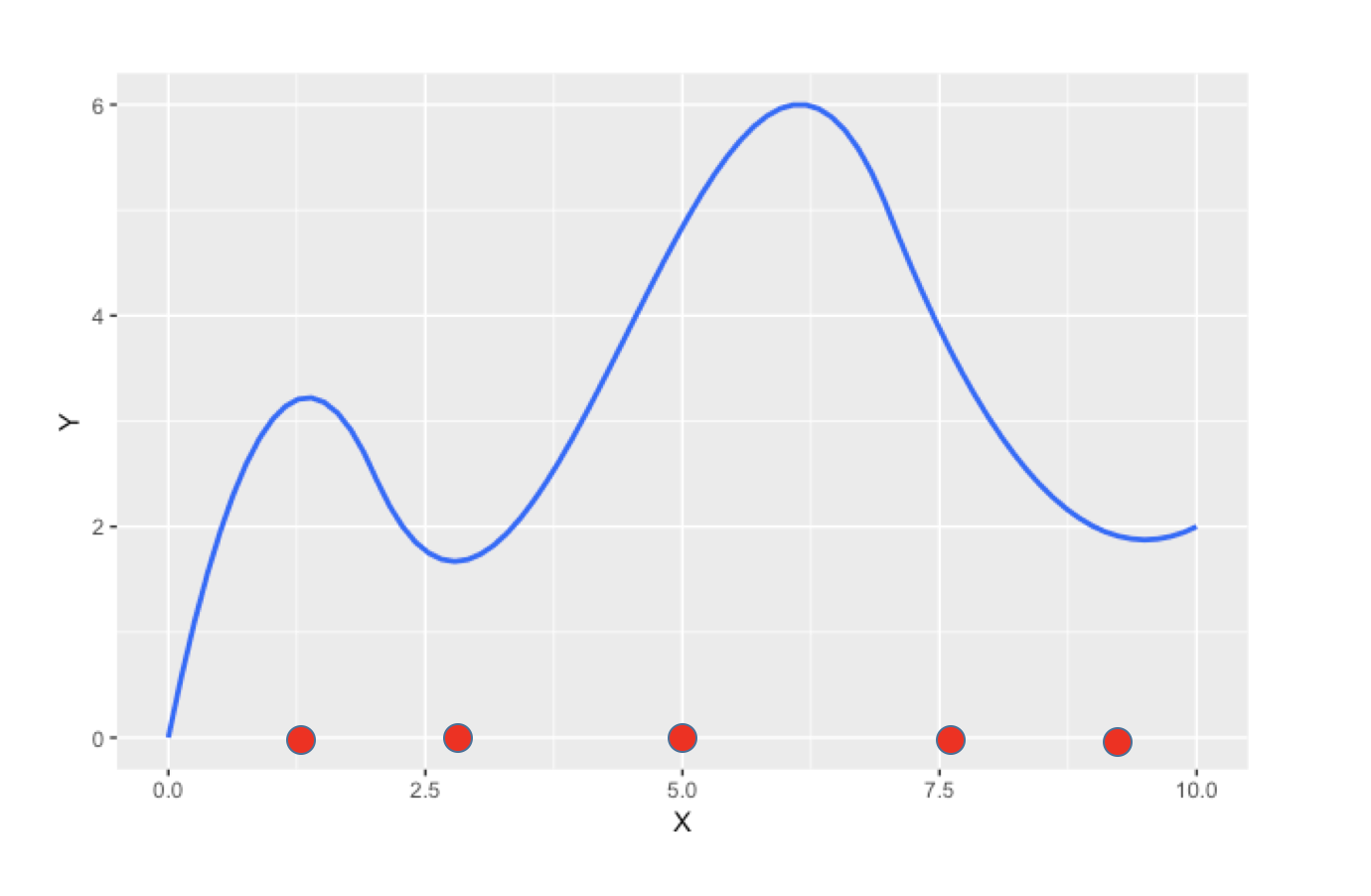
如上图所示，X轴是整个解空间（没错，并且还是连续的，不过只能取整数），Y轴是我们期望达到的最短路径值。

初始情况，我们会随机的在解空间挑选几个点。

3.2 评估种群个体的适应度

很明显对于旅行商问题，整个路径越短，适应度越高（Y轴）

3.4 交叉

交叉是为了进行种群的繁殖。并且交叉的过程会保留亲代的特征。通常获得的下一代会在亲代的坐标点附近。

常见的交叉算法
1. 单点杂交
2. 多点杂交
3. 均匀杂交
4. 洗牌杂交
在我的代码实现中，我使用的是单点交叉

3.5 变异

近亲繁殖容易导致畸形儿。近亲的交叉，会使得子代聚集在它们附近，从而收敛在次优解上，而忽略了真正的最优解。
为了避免这个问题，引入变异。
变异的具体做法，是对解对应数值的2进制表示的某一位进行翻转，0变成1，1变成0。

变异带来的直接效果是，子代的值会在x轴（解空间）上跳跃，种群中的个体在解空间分布的更加随机，增强了种群的多样性。

3.6 选择

如果不控制种群的数量，在解空间较小的情况下，种群的规模有可能会覆盖整个解空间。

由于每次迭代（交叉和变异）非常耗时，所以有必要限制种群的规模。

希望达到的效果

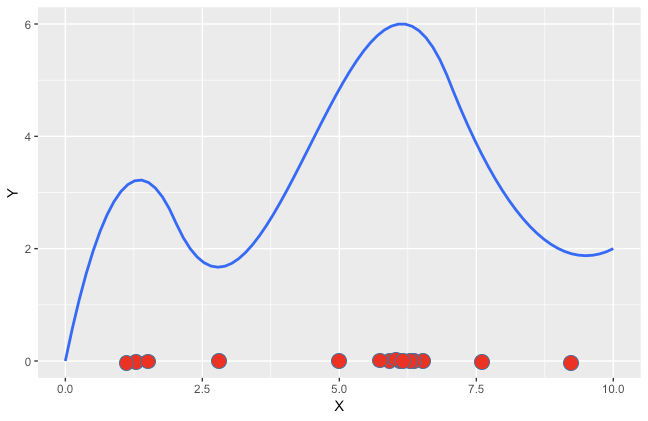
经过若干次迭代，种群中的个体，将会大量分布在最优解以及次优解附近。

常见选择算法
1. 轮盘选择算法 roulette wheel selection
2. 锦标赛选择算法 tournament selection
3. 随机遍历抽样算法

需要注意的问题:
选择算法不能简单的将个体的适应度排序，然后剔除适应度最差的节点。这样有可能会导致种群失去多样性，而最终收敛在次优解上。

从人类社会的演化，我们似乎能找到某种共同性。比如如果按照指令性的方式去管理经济，得到的是高效服从命令的企业，但是整个社会又会缺乏创造性。

4. 样例代码

test2.go

...

func main() {
    positions := []string{"北京", "天津", "上海", "重庆", "拉萨", "乌鲁木齐",
        "银川", "呼和浩特", "南宁", "哈尔滨", "长春", "沈阳", "石家庄",
        "太原", "西宁"}
    // 最大迭代次数
    maxIterCount := tsp.MaxIterationCountOption(200)
    // 种群中最大个体数量
    maxPopulationSize := tsp.MaxPopulationSizeOption(1000)
    // 设置选择算法
    selectFunc := tsp.SelectAlgOption(tsp.RandomTraverseSampleSelection)
    //selectFunc := tsp.SelectAlgOption(tsp.RouletteWheelSelection)
    //selectFunc := tsp.SelectAlgOption(tsp.TournamentSelection)

    t := tsp.NewTSP(positions, distance2, maxIterCount, maxPopulationSize, selectFunc)
    result := t.Slove()
    fmt.Println("---result---:", result, "route distance", t.RouteDistance(result))
    // 输入到文件，以便绘图观察
    write2File(result, "/tmp/1.csv")

}
...

5. 绘图

可以使用R语言来绘制路径图

library(ggplot2)
data = read.table("/tmp/1.csv",header=F, sep=",")
traveller_way = read.table("/tmp/1.csv",header=TRUE, sep=",")

m <- ggplot(traveller_way, aes(X, posY))
m + geom_path()

经过200次迭代,花费的时间是6.5秒,就找到15个城市的旅行商问题的解决方案,遗传算法还是非常高效的。

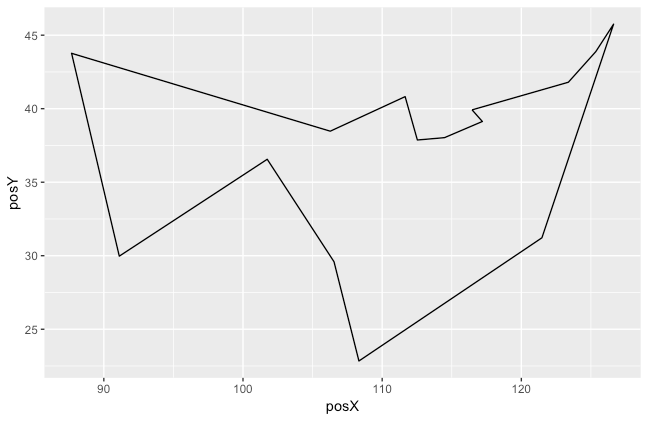
6 传送门

项目地址
vearne/tsp

7. 参考资料

1. 遗传算法
2. 旅行商问题
3. 遗传算法详解

---

请我喝瓶饮料