算法题(9)

版权声明 本站原创文章 由 萌叔 发表
转载请注明 萌叔 | https://vearne.cc

问题描述

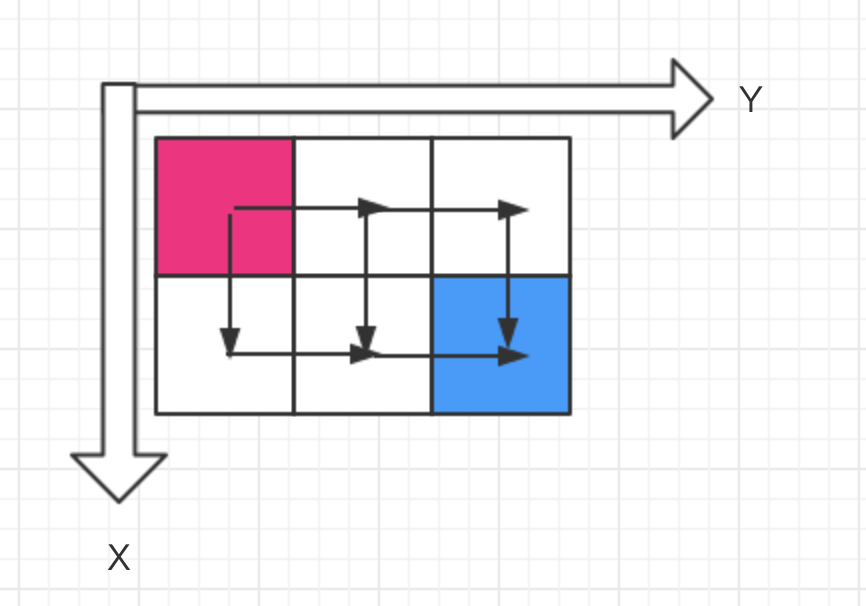
如下图所示，从矩阵(m*n)的(0， 0)出发，然后只能向下、向右，到达矩阵的对角（m-1, n-1）

求从(0,0)到(m-1, n-1) 一共有多少种走法

解题思路

解决这个问题，我们可以参考动态规划的思想
要到达(m-1, n-1), 就必须到达(m-2, n-1)或者(m-1, n-2)
从(m-2, n-1)到(m-1, n-1) 只有一种走法
从(m-1, n-2)到(m-1, n-1) 只有一种走法
那么从(0, 0)到(m-1, n-1)的走法数量

f(m-1, n-1) = f(m-2, n-1) + f(m-1, n-2)

递归算法

采用递归算法可以很容易写出代码

def try_walk(m, n):
    if m == 1 and n == 1:
        return 0
    return walk(m -1, n -1)

def walk(x, y):
    if x == 0 and y == 0:
        return 1

    res = 0
    if x - 1 >= 0:
        res += walk(x - 1, y)

    if y - 1 >= 0:
        res += walk(x, y - 1)

    return res

if __name__ == '__main__':
    print (1,1), try_walk(1, 1)
    print (1,2), try_walk(1, 2)
    print (2,2), try_walk(2, 2)
    print (2,3), try_walk(2, 3)
    print (3,3), try_walk(3, 3)

参考动态规划的思想，可以记录cache (x,y)到(0,0) 走法的数量，加快速度

def try_walk(m, n):
    if m == 1 and n == 1:
        return 0

    matrix = []
    for i in range(m):
        a = []
        for j in range(n):
            a.append(-1)
        matrix.append(a)

    return walk(m -1, n -1, matrix)

def walk(x, y, matrix):

    if x == 0 and y == 0:
        return 0

    # print(x, y)
    if matrix[x][y] != -1:
        return matrix[x][y]

    res = 0
    if x - 1 >= 0:
        res += walk(x - 1, y, matrix)

    if y - 1 >= 0:
        res += walk(x, y - 1, matrix)

    return res

if __name__ == '__main__':
    print (1,1), try_walk(1, 1)
    print (1,2), try_walk(1, 2)
    print (2,2), try_walk(2, 2)
    print (2,3), try_walk(2, 3)
    print (3,3), try_walk(3, 3)

非递归算法

由于要计算出f(x, y)，必须先算出计算出f(x -1, y) 和f(x, y - 1)
(x - 1, y) 在 (x, y) 的上边， (x, y - 1) 在 (x, y) 的左边
因此只需要按矩阵，逐行, 每行中再逐列计算即可

def try_walk(m, n):
    if m == 1 and n == 1:
        return 0

    matrix = []
    for i in range(m):
        a = []
        for j in range(n):
            a.append(0)
        matrix.append(a)

    matrix[0][0] = 1
    for i in range(m):
        for j in range(n):
            if i - 1 >= 0:
                matrix[i][j] += matrix[i-1][j]
            if j - 1 >= 0:
                matrix[i][j] += matrix[i][j - 1]

    return matrix[m-1][n-1]


if __name__ == '__main__':
    print (1,1), try_walk(1, 1)
    print (1,2), try_walk(1, 2)
    print (2,2), try_walk(2, 2)
    print (2,3), try_walk(2, 3)
    print (3,3), try_walk(3, 3)

请我喝瓶饮料